Stochastic Analysis of the Marginal and Dependence Structure of Streamflows: From Fine-Scale Records to Multi-Centennial Paleoclimatic Reconstructions

Abstract

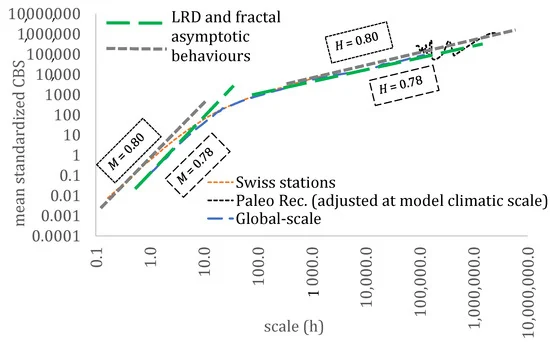
The identification of the second-order dependence structure of streamflow has been one of the oldest challenges in hydrological sciences, dating back to the pioneering work of H.E Hurst on the Nile River. Since then, several large-scale studies have investigated the temporal structure of streamflow spanning from the hourly to the climatic scale, covering multiple orders of magni-tude. In this study, we expanded this range to almost eight orders of magnitude by analysing small-scale streamflow time series (in the order of minutes) from ground stations and large-scale streamflow time series (in the order of hundreds of years) acquired from paleocli-matic reconstructions. We aimed to determine the fractal behaviour and the long-range de-pendence behaviour of the streamflow. Additionally, we assessed the behaviour of the first four marginal moments of each time series to test whether they follow similar behaviours as sug-gested in other studies in the literature. The results provide evidence in identifying a common stochastic structure for the streamflow process, based on the Pareto–Burr–Feller marginal dis-tribution and a generalized Hurst–Kolmogorov (HK) dependence structure.

Alonso Pizarro

Professor of Hydrology & Hydraulics

My research interests include Hydraulics, Hydrology, Stochastic processes in Hydrology, Fluvial monitoring, UASs, Bridge scour